Stroboscope
I present here an outreach experiment I produced for the nuit de la science in 2016 in Geneva.
It is an experiment allowing to speak about stroboscopic effect, persistence of vision, temporal resolution in time resolved spectroscopy, and explaining why the car wheels turn sometimes backward in the movies…
The general idea is simple: a pattern is turning, and strong LEDs are flashing at a given frequency. The fun phenomena occur when the flashing frequency is close or equal to a multiple of the turning frequency.
The main advantage of this experimental setup is that it allows the user to directly set and see the ratio between the flash frequency and the rotation frequency of the pattern. It is set by the command pad, and display by the red digits in the upper right corner. It eases a lot the explanations.
How does it work
On the NASA style command pad, the user can set the integer and the first decimal of the ratio between the flash frequency and the turning frequency. The image is turning at around 40Hz, to avoid visual blinking.
Simple patterns
As our vision persistence is about 1/10 seconds. It means that our eyes are not able to distinguish two events separated by less than one tenth of second. As a results, if the image is turning fast, and the flashes are synchronized with the turning frequency, it yields a fixed image:
Here is a tiny gif animation explaining the phenomenon in slow motion: the grey circles are the moving image. The red blink is the flash, and the white circles is the pattern of the superposition of what stays in our retina because of vision persistence.


Of course, the resulting pattern depends on the number of flashes per image turn. If you increase the number of flashes, it results in more “branches” in the persistent pattern.
Turning patterns
If now the flashing frequency is not a multiple of the turning frequency…
Well, the pattern will be slightly shifted at each flash, in one direction or the other. It depends if the flash occurs before or after the pattern completed an entire turn. The resulting image will appear to turn at a speed that depends on the difference between the turning frequency and the flashing frequency.

It is exactly what happen when the car wheel turn backward in a movie: the camera acts like a stroboscope flashing at 1/24 Hz (24 images per second), a frequency that is not a multiple of the car wheel.
More complex patterns
Let’s try with some more complex pattern.
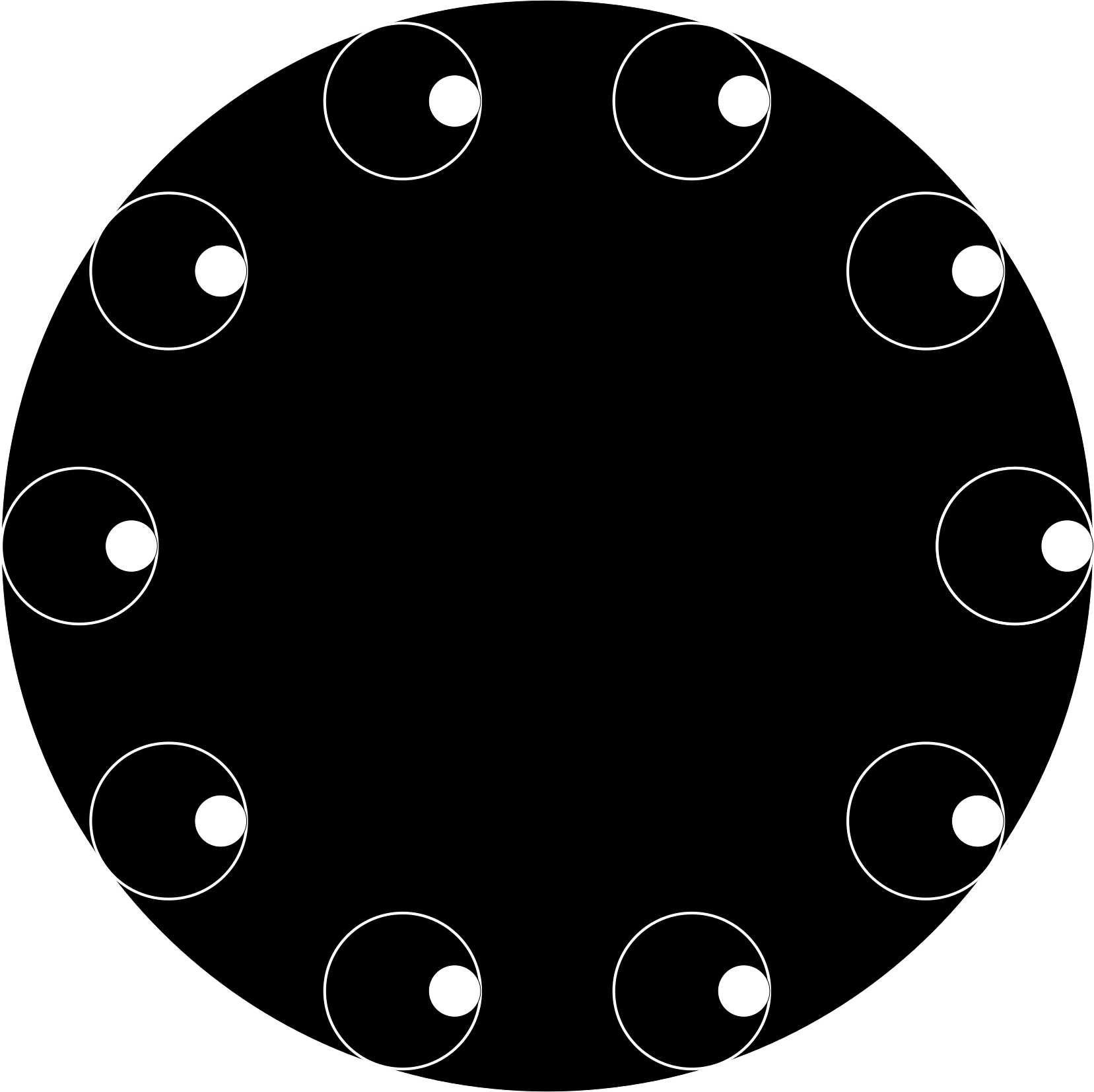
Here I have 10 white circles with dots inside. Similar to what I have shown before, if I set the flashing frequency to a multiple of the turning frequency, I obtain theses kind of figures
If we now set the flash frequency so that the flash occurs when the pattern does one turn + 1/10 of a turn, we re-invent the zootrope, ancestor of the movie:
Let’s propose a slow-motion explanation: in grey is pictured the moving image, the red blink is the flash, and the white image is the pattern captured by the retina of your eyes (and staying 1/10 second, so longer than the time between two flashes). The grey bar indicates the position of the initial top circle during the movement.
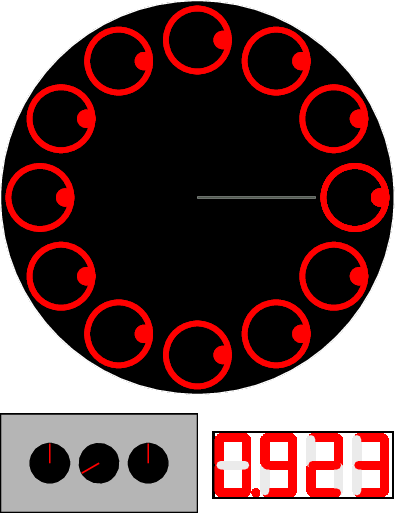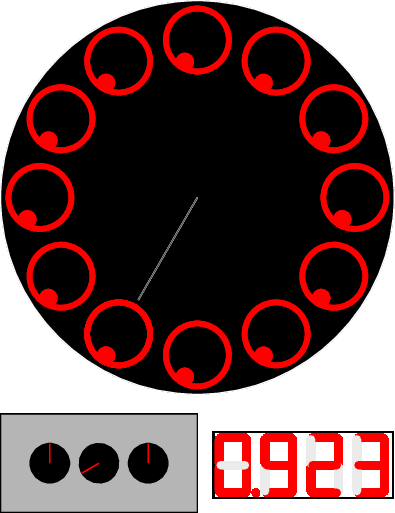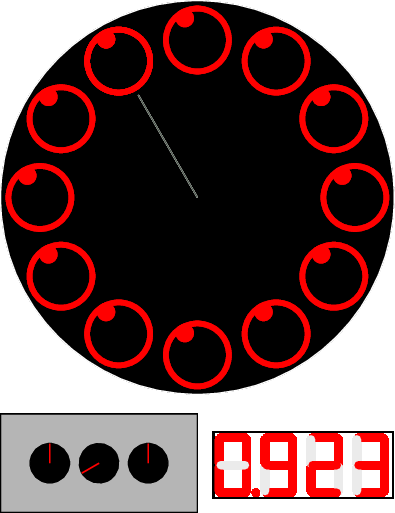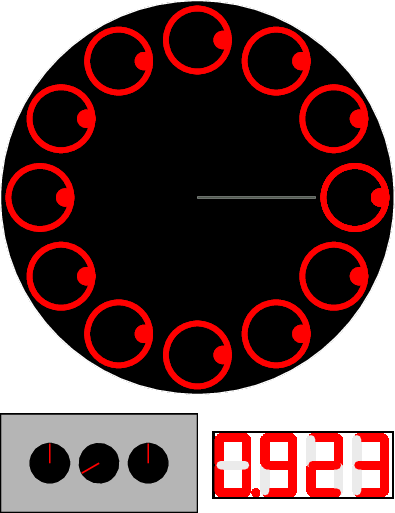
The successive circles with the white dot inside are not identical: they are turned by 1/10th of a turn. The flashes produce then an apparent movement of the white dot.
The light flash must be short to freeze the fast-moving pattern. Our eye see the moving pattern during the whole flash duration. If the flash if long (or the moving pattern too fast), then the perceived image is blurred. This is a nice illustration of the importance of having short pulses to observe fast phenomenon, and this is why some physicists try to get laser pulses as short as few femtoseconds or below (femtosecond = $10^{-15}s$ = 1 billionth millionth second) to observe molecular motion, or changes of molecular electronic configuration.
Manufacturing the experiment

Some parts were 3D printed, and I did a 3D model to test the assembly with Fusion 360. The images turning on the device have been produced with Latex, and so were the gif animations presented on this page (!!!).
I will soon make several posts to give the arduino code, the detail of the electronic, the bill of material, and the latex code for the images and animations.

